ReasonLines provides (1) a new and easier approach to the traditional syllogism and (2) an expansion of the traditional syllogism to include numerical quantification.
1)The new approach to the traditional syllogism
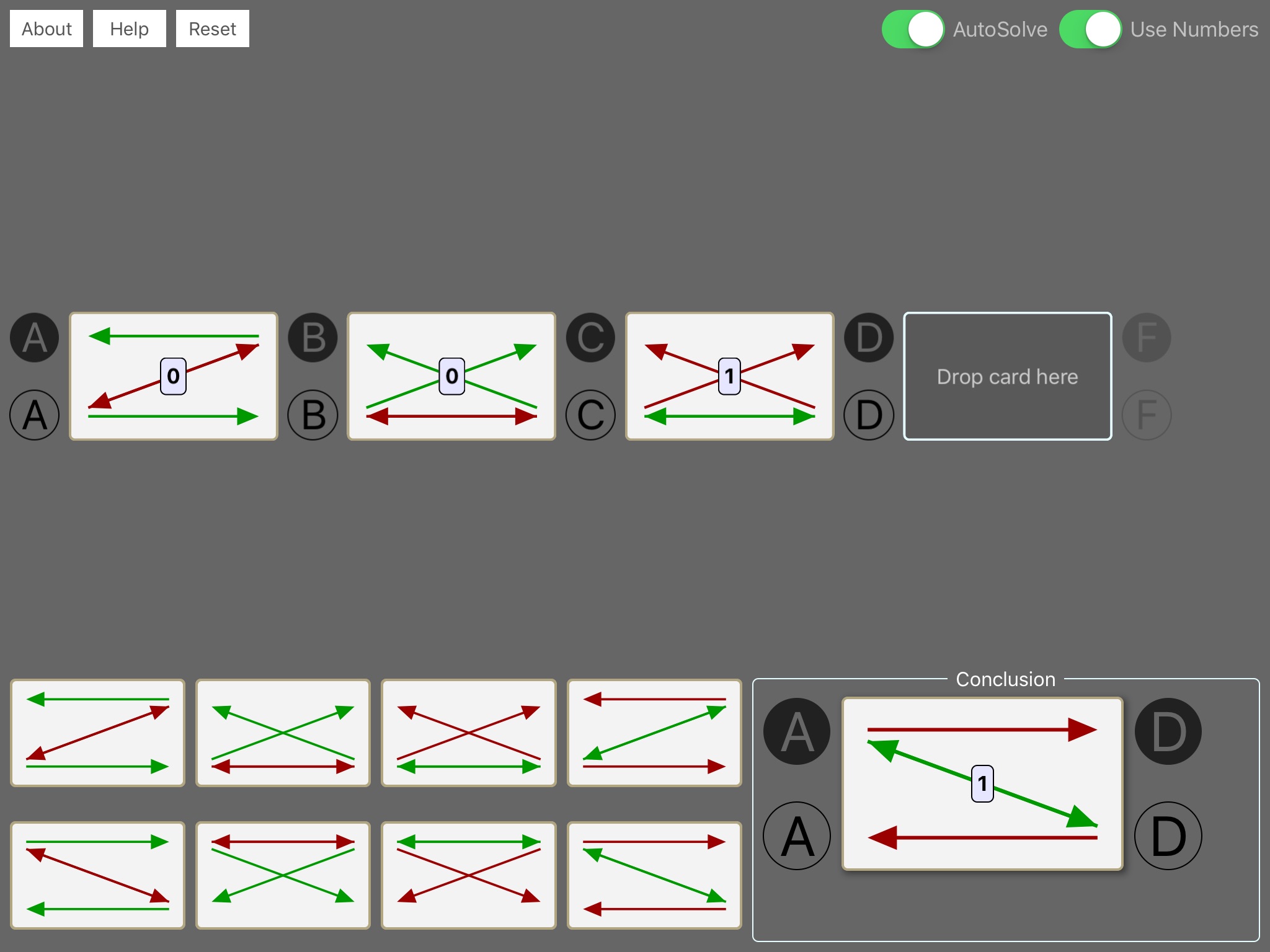
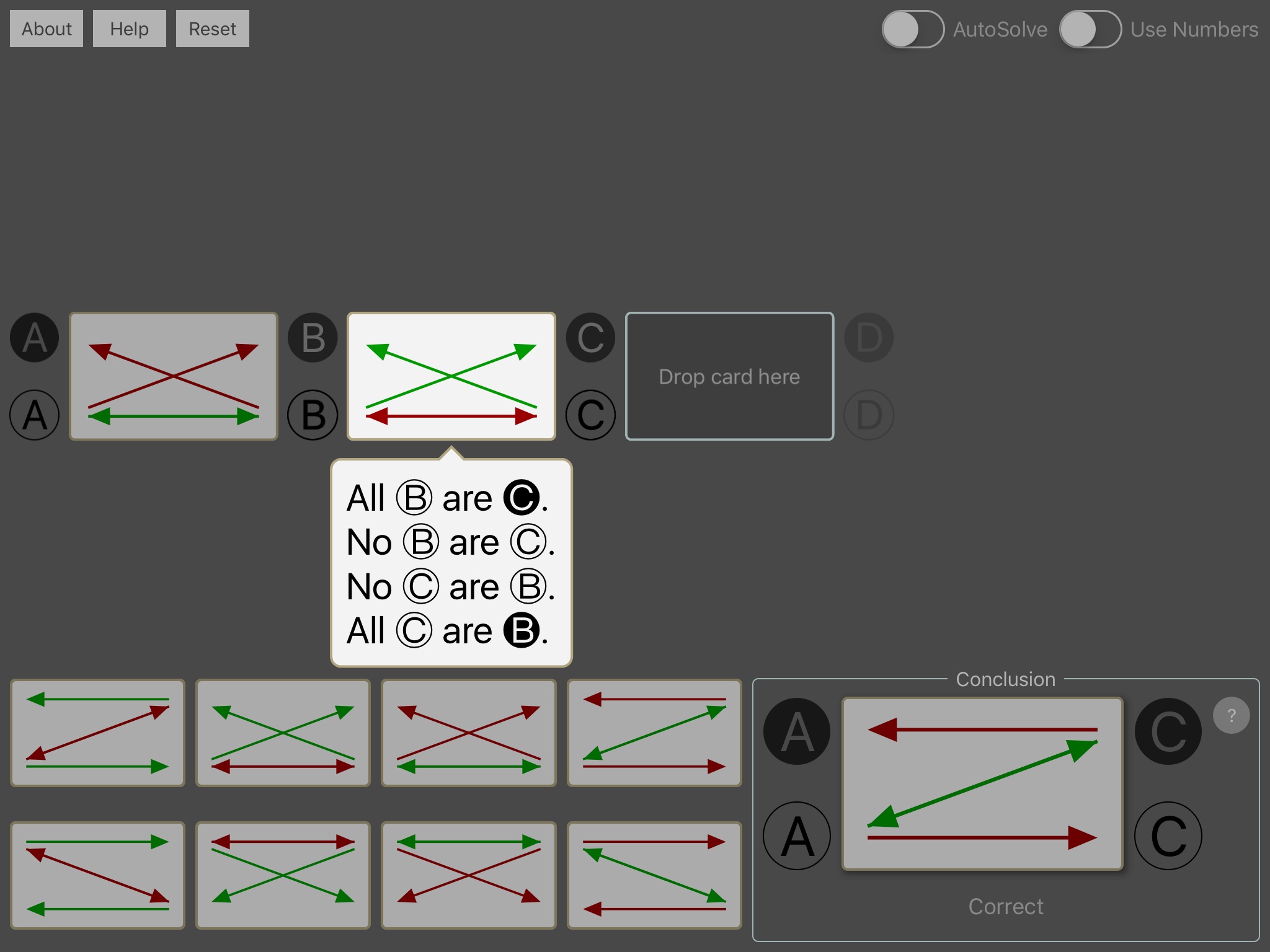
Instead of considering isolated statements as the components of arguments, such as major premise, minor premise, and conclusion, this new approach bundles each statement with its equivalents and each bundle is represented by its own “schematic” of arrows. The premise schematics can then be dropped in place along side each other where their juxtaposition displays whatever conclusion, if any, is entailed. The user only needs to learn how to select the correct premise schematics and how to follow the arrows for a conclusion.
Part One of the Help page is a tutorial for this new approach.
(2)The numerical expansion of the traditional syllogism
It is already standard to interpret the particular quantifier numerically; that is, it is standard to take “some” as “at least one.” Moreover, the universal quantifiers, “all” and “no,” can also be faithfully rendered numerically since “all” means “all with zero exception” and “no” means none “none with zero exception.” Given this, it turns out that the traditional quantifiers simply mark the beginnings of endless possible quantifications since “at least one” opens the series of “at least two,” “at least three,” etc., and “all (none) but zero” opens “all (none) but one,” “all (none) but two,” etc.
By making this explicit, the zero and one of traditional syllogisms become replaceable by other numbers. So, for example, “All but 10 A are B and all but 20 B are C, so All but 30 A are C,” and “At least 100 A are B, All but 7 B are C, so At least 93 A are C,” are just as valid as the traditional Barbara and Darii, and for the very same reason.
Part Two of the Help page develops this numerical expansion by appealing to the schematics.